

Real Statistics Data Analysis Tool: The Multiple Linear Regression data analysis tool described in Real Statistics Capabilities for Linear Regression provides an option to test the normality of the residuals.įor Example 2 of Multiple Regression Analysis in Excel, this is done by selecting the Normality Test option on the dialog box shown in Figure 1 of Real Statistics Capabilities for Linear Regression. Thus, the values in the range AC4:AC14 of Figure 1 can be generated via the array formula RegStudE(A4:B14,C4:C14), again referring to the data in Figure 3 of Method of Least Squares for Multiple Regression Data Analysis Tool RegStudE(R1, R2) = n × 1 column array of studentized residuals Real Statistics Function: The Real Statistics Resource Pack provides the following array function where R1 is an n × k array containing X sample data and R2 is an n × 1 array containing Y sample data. Also, some of this might be due to the presence of outliers (see Outliers and Influencers). The values are reasonably spread out, but there does seem to be a pattern of rising value on the right, but with such a small sample it is difficult to tell. We now plot the studentized residuals against the predicted values of y (in cells M4:M14 of Figure 2).įigure 2 – Studentized residual plot for Example 1 See Example 2 in Matrix Operations for more information about extracting the diagonal elements from a square matrix. Where O4:O14 contains the matrix of raw residuals E, and O19 contains MS Res. From H, the vector of studentized residuals is calculated by the array formula Alternatively, H can be calculated using the Real Statistics function HAT(A4:B14). Where E4:G14 contains the design matrix X. We start by calculating the studentized residuals (see Figure 1).įigure 1 – Hat matrix and studentized residualsįirst, we calculate the hat matrix H (from the data in Figure 1 of Multiple Regression Analysis in Excel) by using the array formula ExampleĮxample 1: Check the assumptions of regression analysis for the data in Example 1 of Method of Least Squares for Multiple Regression by using the studentized residuals. With multiple independent variables, then the plot of the residual against each independent variable will be necessary, and even then multi-dimensional issues may not be captured. This approach works quite well where there is only one independent variable. If this is not the case then one of these assumptions is not being met. It should also be noted that if the linearity and homogeneity of variances assumptions are met then a plot of the studentized residuals should show a randomized pattern. In particular, we can use the various tests described in Testing for Normality and Symmetry, especially QQ plots, to test for normality, and we can use the tests found in Homogeneity of Variance to test whether the homogeneity of variance assumption is met. We can now use the studentized residuals to test the various assumptions of the multiple regression model. Where n = the number of elements in the sample and k = the number of independent variables. If the ε i have the same variance σ 2, then the studentized residuals have a Student’s t distribution, namely Studentized Residualsĭefinition 1: The studentized residuals are defined by As usual, MS Ecan be used as an estimate for σ. If, however, the h iiare reasonably close to zero then the r i can be considered to be independent. The r ihave the desired distribution, but they are still not independent. Unfortunately, the raw residuals are not independent.īy Property 3b of Expectation, we know that It turns out that the raw residuals e i follow a normal distribution with mean 0 and variance σ 2(1- h ii) where the h ii are the terms in the diagonal of the hat matrix defined in Definition 3 of Method of Least Squares for Multiple Regression. It is natural, therefore, to test our assumptions for the regression model by investigating the sample observations of the residuals If these assumptions are satisfied then the random errors ε i can be regarded as a random sample from an N(0, σ 2) distribution. Homogeneity of variances: The ε ihave the same variance σ 2.Normality: The ε i are normally distributed.
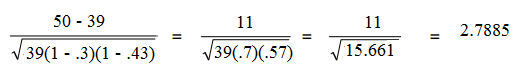

In Multiple Regression Analysis, we note that the assumptions for the regression model can be expressed in terms of the error random variables as follows:


 0 kommentar(er)
0 kommentar(er)
